การเข้ารหัสทางประสาท

การยิงศักยะงานเป็นขบวนหรือเป็นลำดับ ๆ ของเซลล์ประสาท

การเข้ารหัสทางประสาท (อังกฤษ: Neural coding) เป็นการศึกษาทางประสาทวิทยาศาสตร์ เพื่อกำหนดความสัมพันธ์ระหว่างสิ่งเร้ากับการตอบสนองของเซลล์ประสาทเดี่ยว ๆ หรือของกลุ่มเซลล์ประสาท และความสัมพันธ์ระหว่างการทำงานทางไฟฟ้าของเซลล์ประสาทในกลุ่ม โดยอาศัยทฤษฎีว่า การทำงานของเครือข่ายเซลล์ประสาทในสมองจะเป็นตัวแทนข้อมูลทางประสาทสัมผัสและข้อมูลอื่น ๆ นักวิชาการจึงเชื่อว่า เซลล์ประสาทสามารถเข้ารหัสข้อมูลเป็นทั้งแบบดิจิตัลและแบบแอนะล็อก

มุมมองกว้าง ๆ

กราฟแสดงศักยะงานทั่ว ๆ ไปหนึ่งอิมพัลส์ ซึ่งแสดงเฟสต่าง ๆ ของศักยะงาน ขบวนศักยะงานก็คือศักยะงานหลายอิมพัลส์ส่งต่อ ๆ กันโดยมีช่องเว้นทางเวลาที่ต่าง ๆ กัน

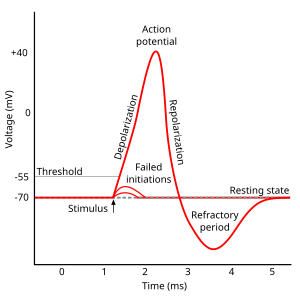
เซลล์ประสาทค่อนข้างจะน่าทึ่งในบรรดาเซลล์ต่าง ๆ ในร่างกาย เพราะสามารถส่งสัญญาณไปอย่างรวดเร็วได้ระยะไกล ๆ ซึ่งดำเนินการโดยอาศัยอิมพัลส์ไฟฟ้าที่เรียกว่า ศักยะงาน ซึ่งส่งไปตามใยประสาท เซลล์ประสาทรับความรู้สึกจะส่งขบวนศักยะงานเป็นจังหวะตามกาลเวลาที่ต่าง ๆ กัน เพื่อตอบสนองต่อสิ่งเร้าภายนอกเช่น แสง เสียง รส กลิ่น และสัมผัส ข้อมูลเกี่ยวกับสิ่งเร้าจะเข้ารหัสเป็นขบวนศักยะงานเช่นนี้ แล้วส่งไปยังทั้งสมองและรอบ ๆ สมอง

แม้ศักยะงานอาจจะต่างกันบ้างเช่นระยะห่างของแต่ละอิมพัลส์ แอมพลิจูด และรูปร่าง แต่งานศึกษารหัสทางประสาทจะปฏิบัติต่อพวกมันเหมือนกับเป็นเหตุการณ์ที่มีรูปแบบตายตัวและเหมือนกัน ถ้าไม่สนใจระยะการดำรงอยู่ของศักยะงาน (ประมาณ 1 มิลลิวินาที) ขบวนหรือลำดับศักยะงาน จะมีลักษณะเป็นลำดับข้อมูลแบบมีหรือไม่มี (all-or-none) คล้าย ๆ สัญญาณดิจิทัล ช่องว่างระหว่างอิมพัลส์ศักยะงานบ่อยครั้งจะต่างกัน โดยดูเหมือนจะเป็นไปโดยสุ่ม การศึกษารหัสทางประสาทจะอาศัยการวัดและกำหนดว่า ลักษณะต่าง ๆ ของสิ่งเร้า เช่นความสว่างของแสง ความดังของเสียง การทำงานของกล้ามเนื้อเช่นทิศทางการเคลื่อนไหวของแขน จะสามารถกำหนดโดยขบวนศักยะงานในเซลล์ประสาทได้อย่างไร เพื่อกำหนดและวิเคราะห์การยิงศักยะงานของเซลล์ประสาท นักวิทยาศาสตร์มักนิยมใช้วิธีการทางสถิติศาสตร์ ทางทฤษฎีความน่าจะเป็น และ stochastic point process

เมื่อมีพัฒนาการของเทคโนโลยีเพื่อบันทึกและถอดรหัสสัญญาณประสาทดีขึ้น ๆ นักวิทยาศาสตรจึงเริ่มเข้าใจสัญญาณทางประสาทได้มากขึ้น ทำให้เริ่มเห็นแสงรำไร ๆ เกี่ยวกับรหัสประสาทตามเวลาจริงเมื่อมีการสร้างและการระลึกถึงความจำในฮิปโปแคมปัส ซึ่งเป็นศูนย์สมองเกี่ยวกับการสร้างความจำ และนักประสาทวิทยาศาสตร์ก็ได้ริเริ่มโครงการถอดรหัสสัญญาณสมองขนาดใหญ่หลายโครงการ

การเข้าและการถอดรหัส

ความสัมพันธ์ระหว่างสิ่งเร้ากับการตอบสนองของระบบประสาทสามารถศึกษาได้จากมุมตรงกันข้าม 2 ด้าน

1. การเข้ารหัสทางประสาท (Neural encoding) ก็คือการแปลสิ่งเร้าเป็นการตอบสนองของเซลล์ประสาท ประเด็นการศึกษาหลักก็เพื่อเข้าใจว่า นิวรอนจะตอบสนองอย่างไรต่อสิ่งเร้าต่าง ๆ แล้วสร้างแบบจำลองเพื่อใช้พยากรณ์การตอบสนองต่อสิ่งเร้าอื่น ๆ
2. การถอดรหัสทางประสาท (Neural decoding) ก็จะกลับกัน คือเป็นการแปลการตอบสนองทางประสาทเป็นสิ่งเร้า โดยเป้าหมายก็คือการระบุสิ่งเร้า หรือลักษณะบางอย่างของสิ่งเร้านั้น จากขบวนศักยะงานที่เซลล์ประสาทสร้างเพื่อตอบสนอง

สมมติฐานการเข้ารหัสต่าง ๆ

ขบวนหรือลำดับศักยะงานอาจมีข้อมูลที่เข้ารหัสโดยแผนการต่าง ๆ กัน เช่น ในเซลล์ประสาทสั่งการ (motor neuron) กล้ามเนื้อที่เชื่อมกับเซลล์ประสาทจะออกแรงโดยขึ้นอยู่กับอัตราการยิงศักยะงานเท่านั้น ซึ่งก็คือจำนวนศักยะงานต่อช่วงเวลาหนึ่ง ๆ โดยเฉลี่ย นี่เป็นการเข้ารหัสโดยอัตรา (rate coding) ในนัยตรงกันข้าม รหัสโดยเวลา (temporal code) ที่ซับซ้อนจะขึ้นอยู่กับการยิงสัญญาณในช่วงเวลาแต่ละระยะ ๆ อย่างแม่นยำ ซึ่งอาจเกิดเพราะจับคู่กับสิ่งเร้าภายนอก ดังที่พบในระบบการเห็น และระบบการได้ยิน หรืออาจเกิดในวงจรประสาทเองโดยธรรมชาติ

ประเด็นว่า นิวรอนจะใช้รหัสโดยอัตรา หรือรหัสโดยเวลา เป็นเรื่องที่ได้ความสนใจอย่างมากภายในชุมชนนักประสาทวิทยาศาสตร์ แม้จะยังไม่มีนิยามที่แน่นอนว่า คำเหล่านี้หมายความว่าอะไร ในทฤษฎีหนึ่งที่เรียกว่า neuroelectrodynamics (พลวัตทางประสาทไฟฟ้า) การเข้ารหัสที่จะกล่าวต่อไปเหล่านี้ล้วนพิจารณาว่าเป็นอนุปรากฏการณ์ (epiphenomena) ซึ่งมีเหตุจากการเปลี่ยนแปลงในระดับโมเลกุลที่สะท้อนการกระจายตามพื้นที่ของสนามไฟฟ้าภายในนิวรอน โดยเป็นผลของสเปกตรัมแม่เหล็กไฟฟ้าที่มีพิสัยกว้างของศักยะงาน และข้อมูลจะปรากฏเป็น spike directivity

การเข้ารหัสโดยอัตรา (Rate coding)

แบบจำลองการเข้ารหัสโดยอัตราเพื่อสื่อข้อมูลเสนอว่า เมื่อระดับของสิ่งเร้า (เช่นความสว่างของแสง) เพิ่มขึ้น อัตราของศักยะงานที่เซลล์ส่งก็จะเพิ่มขึ้นด้วย การเข้ารหัสโดยอัตรา (Rate coding) บางครั้งก็เรียกว่า การเข้ารหัสโดยความถี่ (frequency coding) ด้วยเหมือนกัน

รหัสนี้เป็นแบบดั้งเดิม โดยสมมุติว่า ข้อมูลเกี่ยวกับสิ่งเร้าเกือบทั้งหมดหรือทั้งหมดจะเข้ารหัสเป็นอัตราของศักยะงาน แต่เพราะลำดับการส่งศักยะงานตอบสนองต่อสิ่งเร้าหนึ่ง ๆ จะเปลี่ยนไปเมื่อทดลองแต่ละครั้ง ๆ การตอบสนองของเซลล์จึงต้องดำเนินการโดยวิธีการทางสถิติหรือตามความน่าจะเป็น และกำหนดข้อมูลเป็นอัตราการยิงสัญญาณ ไม่ใช่ลำดับการยิงสัญญาณโดยเฉพาะ ๆ ในระบบรับความรู้สึกส่วนมาก โดยทั่วไปอัตราการยิงสัญญาณจะเพิ่มขึ้นแบบไม่ใช่เชิงเส้นตามระดับของสิ่งเร้า

แบบจำลองนี้จะไม่ให้ความสำคัญแก่ข้อมูลที่ระบบประสาทอาจเข้ารหัสเป็นระยะเวลาในระหว่างขบวนศักยะงาน ดังนั้น รหัสโดยอัตราจึงมีประสิทธิภาพที่ไม่ดี แต่ก็ทนทานต่อเสียงรบกวนได้ดีมาก (เหมือนสัญญาณดิจิทัล) เมื่อเข้ารหัสโดยอัตรา การคำนวณอัตราศักยะงานอย่างแม่นยำจะเป็นเรื่องสำคัญมาก และจริง ๆ แล้ว คำว่า อัตราการยิงสัญญาณ (firing rate) ก็มีหลายความหมายหลายนิยาม โดยต่างกันตามวิธีหาค่าเฉลี่ย เช่น ค่าเฉลี่ยตามเวลา หรือค่าเฉลี่ยที่ได้จากการทดลองที่ทำซ้ำ ๆ

เมื่อเข้ารหัสโดยกระบวนการนี้ การเรียนรู้จะเกิดผ่านการเปลี่ยนความสำคัญของสัญญาณที่ส่งผ่านไซแนปส์โดยขึ้นอยู่กับการทำงาน (activity-dependent synaptic weight modifications)

นักสรีรวิทยาไฟฟ้าชาวอังกฤษ ดร. เอ็ดการ์ เอเดรียน และนักสรีวิทยาประสาทชาวสวีเด็น Yngve Zotterman ได้แสดงการเข้ารหัสของประสาทโดยอัตราเป็นครั้งแรกในปี พ.ศ. 2469 การทดลองดั้งเดิมนี้ได้แขวนน้ำหนักขนาดต่าง ๆ จากกล้ามเนื้อ เมื่อน้ำหนักเพิ่มขึ้น อัตราการส่งศักยะงานจากเส้นประสาทรับความรู้สึกที่อยู่ในกล้ามเนื้อก็เพิ่มขึ้นด้วย จากงานทดลองดั้งเดิมนี้ นักวิทยาศาสตร์ทั้งสองจึงสรุปว่า ศักยะงานเป็นเหตุการณ์เดี่ยว ๆ และความถี่ของการเกิดเหตุการณ์ ไม่ใช่ขนาดของเหตุการณ์แต่ละเหตุการณ์ ๆ เป็นมูลฐานการสื่อสารระหว่างนิวรอน

ในทศวรรษต่อ ๆ มา การวัดอัตราการส่งสัญญาณกลายเป็นมาตรฐานเพื่อระบุคุณสมบัติต่าง ๆ ของเซลล์ประสาทรับความรู้สึกและเซลล์ประสาทในเปลือกสมองส่วนต่าง ๆ โดยส่วนหนึ่งก็เพราะมันวัดได้ง่ายเทียบกับวิธีอื่น ๆ แต่วิธีนี้ก็ไม่สนใจข้อมูลอื่น ๆ ที่อาจจะมาจากระยะการส่งสัญญาณอย่างแม่นยำของนิวรอน งานศึกษาปี 2548 ได้อ้างหลักฐานทางการทดลองต่าง ๆ เพื่อเสนอว่า อัตราการยิงสัญญาณที่เฉลี่ยจำนวนศักยะงานตามกาลเวลาธรรมดา ๆ อาจจะไม่สมบูรณ์พอเพื่ออธิบายการทำงานของสมอง

อัตรานับศักยะงาน (Spike-count rate)

spike-count rate (อัตรานับศักยะงาน) หรือเรียกอีกอย่างว่า temporal average (ค่าเฉลี่ยตามเวลา) วัดได้โดยนับจำนวนศักยะงานที่ปรากฏในช่วงการทดลองเดียวแล้วหารด้วยระยะเวลา ผู้ทำการทดลองจะกำหนด T ซึ่งเป็นระยะเวลา โดยขึ้นกับประเภทนิวรอนที่กำลังบันทึกค่า แต่โดยปกติแล้ว เพื่อให้สมเหตุสมผล ก็จะต้องมีศักยะงานมากกว่าหนึ่งพัลส์ที่เกิดภายในช่วง ดังนั้น ค่า T ปกติจะอยู่ที่ 100 มิลลิวินาที หรือ 500 มิลลิวินาที แต่ก็อาจจะสั้นยาวกว่านั้น

อัตรานับศักยะงานจะกำหนดได้ด้วยการทดลองเพียงแค่ครั้งเดียว แต่ก็แลกกับการไม่ได้รายละเอียดทางเวลาของการตอบสนองที่ต่าง ๆ กันตามธรรมชาติในระยะที่ทำการทดลอง รหัสเช่นนี้จึงดีในกรณีที่สิ่งเร้ามีระดับสม่ำเสมอหรือเปลี่ยนอย่างช้า ๆ โดยสัตว์ไม่จำเป็นต้องตอบสนองอย่างรวดเร็ว ซึ่งเป็นสถานการณ์ที่มักใช้ในเกณฑ์วิธีการทดลองอยู่แล้ว แต่สิ่งเร้าในโลกจริง ๆ แล้วจะไม่ค่อยอยู่นิ่ง ๆ และบ่อยครั้งจะเปลี่ยนอย่างรวดเร็วมาก ยกตัวอย่างเช่น แม้เมื่อดูภาพนิ่ง มนุษย์มักขยับตาแบบ saccade ซึ่งก็คือการเปลี่ยนจุดที่มองอย่างรวดเร็ว ภาพซึ่งตกลงที่เซลล์รับแสงของจอตา ปกติจึงจะเปลี่ยนทุก ๆ ไม่กี่ร้อยมิลลิวินาที

ถึงแม้จะมีข้อบกพร่องเช่นนี้ การเข้ารหัสแบบอัตรานับศักยะงาน ก็ไม่ได้ใช้เพียงแค่ในการทดลองเท่านั้น แต่ยังใช้ในแบบจำลองของโครงข่ายประสาทเทียมอีกด้วย เป็นวิธีที่ทำให้เข้าใจว่า เซลล์ประสาทจะเปลี่ยนข้อมูลเกี่ยวกับตัวแปรขาเข้าอย่างหนึ่ง (คือระดับสิ่งเร้า) ไปเป็นตัวแปรขาออกที่ต่อเนื่องอีกอย่างหนึ่ง (คืออัตราการยิงสัญญาณ)

แต่ก็มีหลักฐานที่เพิ่มขึ้นเรื่อย ๆ ว่า อย่างน้อยที่สุด เซลล์เพอร์คินจีในสมองน้อย ก็ไม่ได้เข้ารหัสข้อมูลด้วยอัตราการยิงสัญญาณเท่านั้น แต่ด้วยเมื่อไร (timing) และระยะ (duration) ที่ไม่ยิงสัญญาณคืออยู่เฉย ๆ ด้วย

อัตราการยิงสัญญาณขึ้นอยู่กับเวลา (time-dependent firing rate)

อัตราการยิงสัญญาณขึ้นอยู่กับเวลา (time-dependent firing rate) นิยามเป็น จำนวนการยิงศักยะงานโดยเฉลี่ย (เฉลี่ยตามการทดลองซ้ำ ๆ) ที่ปรากฏในช่วงเวลาสั้น ๆ ระหว่าง t และ t+Δt แล้วหารโดยช่วงระยะเวลา เป็นการวัดที่ใช้ได้ทั้งสิ่งเร้านิ่ง ๆ และสิ่งเร้าที่เปลี่ยนไปตามเวลา

เมื่อจะวัดค่าอัตราการยิงสัญญาณขึ้นอยู่กับเวลาในการทดลอง ผู้ทำการทดลองจะบันทึกค่าจากนิวรอนเมื่อเร้าด้วยสิ่งเร้าที่ทำเป็นชุด ๆ การเร้าเป็นชุดนี้จะทำซ้ำหลายครั้ง และการตอบสนองของนิวรอนจะบันทึกเป็น Peristimulus time histogram (PSTH) จุดเวลา t จะวัดจากเมื่อเริ่มเร้าด้วยชุดสิ่งเร้า ค่า Δt จะต้องใหญ่พอ (ปกติเริ่มจาก 1 มิลลิวินาทีขึ้น) เพื่อให้มีจำนวนศักยะงานพอประเมินค่าเฉลี่ยอย่างเชื่อถือได้ เมื่อหารด้วยระยะเวลา Δt ก็จะได้ค่า อัตราการยิงสัญญาณขึ้นอยู่กับเวลา r(t) ของนิวรอน ซึ่งเท่ากับความหนาแน่นของศักยะงาน (spike density) ใน PSTH

ถ้า Δt น้อยพอดี r(t) Δt ก็จะเป็นจำนวนศักยะงานโดยเฉลี่ยที่เกิดระหว่าง t จนถึง t+Δt ในการทดลองหลาย ๆ ครั้ง ถ้า Δt มีค่าน้อย ก็จะไม่มีศักยะงานเกินกว่า 1 ในระหว่าง t จนถึง t+Δt ในการทดลองทุกครั้ง ซึ่งก็หมายความว่า r(t) Δt ก็จะมีค่าเป็นเศษส่วนในการทดลองต่าง ๆ ที่บางการทดลองมีศักยะงานหนึ่งพัลส์ในช่วงเวลานั้น หรือโดยเสมอภาคกัน r(t) Δt ก็จะเป็นค่าความน่าจะเป็นที่ศักยะงานหนึ่ง ๆ จะเกิดในช่วงระยะเวลานี้

โดยเป็นวิธีดำเนินการทดลอง อัตราการยิงสัญญาณขึ้นอยู่กับเวลาจะมีประโยชน์เพื่อตรวจการทำงานของเซลล์ประสาท โดยเฉพาะในกรณีที่มีสิ่งเร้าซึ่งขึ้นอยู่กับเวลา ปัญหาโต้ง ๆ ของวิธีนี้ก็คือ มันไม่ใช่วิธีการเข้ารหัสของเซลล์ประสาทในสมอง เพราะมันไม่สามารถรอให้สิ่งเร้าแสดงตัวซ้ำ ๆ ในแบบที่ว่านี้ก่อนจะตอบสนอง

อย่างไรก็ดี ค่านี้จะมีเหตุผล ถ้ามีนิวรอนที่เป็นอิสระต่อกันและกันเป็นกลุ่มใหญ่ ๆ ที่ได้รับสิ่งเร้าเดียวกัน ดังนั้น แทนการบันทึกการตอบสนองจากกลุ่มเซลล์จำนวน N เซลล์ในการทดลองครั้งหนึ่ง การบันทึกการตอบสนองจากเซลล์เดียวแล้วหาค่าเฉลี่ยจากการทดลอง N ครั้ง ก็จะง่ายกว่า ดังนั้น ค่านี้จะมีข้อสมมุติโดยปริยายว่า จะเป็นนิวรอนเป็นกลุ่ม ๆ ที่ตอบสนอง

การเข้ารหัสโดยเวลา (Temporal coding)

เมื่อเวลาที่ส่งศักยะงานหรือความผันผวนของการยิงสัญญาณที่อัตราสูงพบว่ามีข้อมูล รหัสทางประสาทนี้บ่อยครั้งจะกำหนดว่าการเข้ารหัสโดยเวลา (Temporal coding) งานศึกษาจำนวนหนึ่งได้พบว่า รายละเอียดทางเวลาของรหัสอยู่ในระดับมิลลิวินาที ซึ่งแสดงว่า เวลาการส่งศักยะงานที่แม่นยำเป็นส่วนประกอบสำคัญของรหัสทางประสาท การเข้ารหัสข้อมูลเช่นนี้ ซึ่งสื่อผ่านเวลาระหว่างพัลส์ศักยะงานจะเรียกว่า interpulse interval code และมีงานศึกษาจำนวนหนึ่งที่สนับสนุนให้หลักฐาน

ความผันผวนเมื่อยิงสัญญาณที่อัตราสูงของนิวรอน อาจจะเป็นเสียงรบกวนหรืออาจจะเป็นข้อมูลก็ได้ แบบจำลองการเข้ารหัสโดยอัตราเสนอว่า ความไม่สม่ำเสมอเช่นนี้เป็นเสียงรบกวน ส่วนแบบจำลองการเข้ารหัสโดยเวลาเสนอว่า มันเป็นข้อมูล ถ้าระบบประสาทใช้แค่รหัสโดยอัตราเพื่อสื่อข้อมูล อัตราการยิงสัญญาณที่สม่ำเสมอปกติยิ่งกว่านี้ก็ควรจะเป็นข้อได้เปรียบทางวิวัฒนาการ และนิวรอนก็ควรใช้วิธีการนี้และหลีกเลี่ยงวิธีการอื่นที่ไม่ทนเสียงรบกวนเท่า

รหัสโดยเวลาให้คำอธิบายอีกอย่างเกี่ยวกับ "เสียงรบกวน" ว่าเป็นการเข้ารหัสข้อมูลและมีผลต่อการประมวลข้อมูล เพื่อจะจำลองไอเดียนี้ เลขฐานสองสามารถใช้กำหนดช่วงศักยะงาน โดย 1 หมายถึงมีศักยะงาน และ 0 หมายถึงไม่มี รหัสโดยเวลาจะอนุญาตให้ลำดับ 000111000111 มีความหมายต่างจากลำดับ 001100110011 แม้อัตราการยิงสัญญาณของลำดับสองชุดนี้จะเท่ากัน คือ 6 ศักยะงานต่อ/10 มิลลิวินาที

จนกระทั่งเร็ว ๆ นี้ นักวิทยาศาสตร์ปกติจะใช้รหัสโดยอัตราเพื่ออธิบายรูปแบบกระแสประสาทที่เห็นหลังไซแนปส์ (post-synaptic) แต่การทำงานของสมองดูจะต้องแม่นยำตามกาลเวลา เกินกว่าที่รหัสโดยอัตราเพียงอย่างเดียวจะสามารถรองรับได้ กล่าวอีกอย่างก็คือ ข้อมูลสำคัญอาจสูญไปได้เพราะรหัสโดยอัตราไม่สามารถเก็บข้อมูลที่มีทั้งหมดจากขบวนศักยะงาน นอกจากนั้น การตอบสนองจะต่างกันพอสมควรระหว่างสิ่งเร้าที่คล้าย (แต่ไม่เหมือนกัน) ซึ่งแสดงว่า รูปแบบที่ไม่เหมือนกันต่าง ๆ ของขบวนศักยะงานจะมีข้อมูลมากกว่าที่เป็นไปได้ถ้าเป็นรหัสโดยอัตรา

รหัสโดยเวลาจะรวมลักษณะต่าง ๆ ของศักยะงานที่การเข้ารหัสโดยอัตราไม่ได้รวม ยกตัวอย่างเช่น เวลาก่อนเกิดศักยะงานแรกหลังจากที่ได้สิ่งเร้า, ลักษณะต่าง ๆ ที่ขึ้นกับโมเมนต์ทางสถิติที่สองหรือยิ่งกว่านั้นของการแจกแจงความน่าจะเป็นของช่วงระหว่างสิ่งเร้า (Interstimulus interval), ความสุ่มของศักยะงาน, หรือกลุ่มศักยะงานที่ยิงในเวลาที่แม่นยำ (เป็นรูปแบบทางกาลเวลา) ล้วนแต่เป็นข้อมูลที่สามารถใช้เข้ารหัสโดยเวลา

เนื่องจากไม่มีแหล่งอ้างอิงเวลาแบบสัมบูรณ์ภายในระบบประสาท ข้อมูลก็จะต้องเกี่ยวข้องกับเวลาการเกิดศักยะงานโดยเปรียบเทียบภายในกลุ่มนิวรอน หรือกับการแกว่งกวัดของคลื่นสมอง วิธีถอดรหัสโดยเวลาอย่างหนึ่งเมื่อมีการแกว่งกวัดของคลื่นสมอง ก็คือศักยะงานที่ยิงในคาบโดยเฉพาะ ๆ ของวงจรการกวัดแว่ง จะทำให้นิวรอนหลังไซแนปส์ลดขั้วอย่างมีประสิทธิภาพกว่า

โครงสร้างทางเวลาของขบวนศักยะงาน หรืออัตราการยิงสัญญาณ จะกำหนดโดยทั้งการเปลี่ยนแปลงของสิ่งเร้าและกระบวนการเข้ารหัสของนิวรอนเอง สิ่งเร้าที่เปลี่ยนแปลงอย่างรวดเร็วมักจะสร้างขบวนศักยะงานที่มีลักษณะทางเวลาที่แม่นยำและอัตราการยิงสัญญาณที่เปลี่ยนอย่างรวดเร็ว ไม่ว่าระบบจะใช้รหัสอะไรก็ตาม รหัสโดยเวลาจะส่องรายละเอียดทางเวลาในการตอบสนองที่ไม่ได้เกิดจากความเปลี่ยนแปลงของสิ่งเร้าเท่านั้น แต่จะสัมพันธ์กับลักษณะต่าง ๆ ของสิ่งเร้าด้วย ปฏิสัมพันธ์ระหว่างสิ่งเร้าและพลวัตของการเข้ารหัส ทำให้ระบุรหัสโดยเวลาได้ยาก

เนื่องกับรหัสทางเวลา การเรียนรู้จะเกิดผ่านการปรับความช้าเร็วของการสื่อผ่านไซแนปส์โดยขึ้นอยู่กับการทำงาน (activity-dependent synaptic delay modifications) การปรับเปลี่ยนเองก็จะต้องขึ้นกับไม่ใช่เพียงแค่อัตราการยิงสัญญาณ (คือรหัสโดยอัตรา) แต่จะขึ้นกับรูปแบบทางกาลเวลาของศักยะงานด้วย (คือรหัสโดยเวลา) คือ นี่อาจเป็นกรณีพิเศษของกระบวนการ spike-timing-dependent plasticity

ปัญหาของการเข้ารหัสโดยเวลา จะต่างอย่างเป็นอิสระจากปัญหาการเข้ารหัสศักยะงานแต่ละพัลส์ ๆ ที่เป็นอิสระจากกันและกัน ถ้าศักยะงานแต่ละพัลส์เป็นอิสระจากพัลส์อื่น ๆ ในขบวน คุณสมบัติทางเวลาของรหัสประสาทจะกำหนดได้โดยอัตราการยิงสัญญาณที่ขึ้นอยู่กับเวลา r(t) และถ้า r(t) เปลี่ยนช้า ๆ ไปตามเวลา นี่ก็เท่ากับการเข้ารหัสโดยอัตรา แต่ถ้าเปลี่ยนไปอย่างรวดเร็ว นี่เป็นการเข้ารหัสโดยเวลา

การเข้ารหัสโดยเวลาในระบบรับความรู้สึก

สำหรับสิ่งเร้าสั้น ๆ อัตราการยิงศักยะงานสูงสุดของเซลล์ประสาทอาจไม่เร็วพอจะสร้างศักยะงานมากกว่าพัลส์เดียว เนื่องจากมีข้อมูลมากเกี่ยวกับสิ่งเร้าสั้น ๆ ภายในศักยะงานเดียวนี้ จึงดูเหมือนว่าเวลาการยิงศักยะงานเองจะต้องสื่อข้อมูลมากกว่าเพียงเป็นความถี่เฉลี่ยของจำนวนศักยะงานตามระยะเวลา

แบบจำลองนี้สำคัญมากในเรื่องการกำหนดตำแหน่งต้นเสียง (sound localization) ซึ่งเกิดในสมองภายในมิลลิวินาที ๆ คือสมองจะต้องดึงข้อมูลมหาศาลจากการตอบสนองค่อนข้างสั้น ๆ ของเซลล์ประสาท นอกจากนั้น ถ้าการยิงสัญญาณในอัตราที่ต่ำเพียงเป็นสิบ ๆ พัลส์ต่อวินาที จะต้องจำแนกจากอัตราที่ใกล้ ๆ กันสำหรับสิ่งเร้าที่ต่างกัน เซลล์ประสาทที่ต้องจำแนกสิ่งเร้าที่ต่างสองอย่างนี้ ก็จะต้องรอหนึ่งวินาทีหรือมากกว่านั้นเพื่อรวบรวมข้อมูลจนเพียงพอ ซึ่งไม่สอดคล้องกับสิ่งมีชีวิตเป็นจำนวนมากที่สามารถจำแนกสิ่งเร้าสองอย่างที่ว่าได้โดยใช้เวลาแค่เป็นมิลลิวินาที ๆ นี่แสดงว่าระบบประสาทไม่ได้ใช้การเข้ารหัสโดยอัตราเพียงอย่างเดียว

เพื่ออธิบายการเข้ารหัสสิ่งเร้าทางตาได้อย่างรวดเร็ว จึงมีการเสนอว่า เซลล์ประสาทในจอตาจะเข้ารหัสข้อมูลเป็นระยะเวลาแฝงระหว่างการเริ่มมีสิ่งเร้ากับการเกิดศักยะงานแรก ซึ่งเรียกว่า latency to first spike โดยรหัสเช่นนี้ก็พบด้วยในระบบการได้ยินและระบบรับความรู้สึกทางกาย ข้อเสียหลักของรหัสนี้ก็คือจะอ่อนไหวต่อความผันผวนของเซลล์ประสาทที่มีอยู่ตามธรรมชาติ

ในคอร์เทกซ์การมองเห็นปฐมภูมิของลิงมาคาก เวลาระหว่างศักยะงานแรกกับการเริ่มมีสิ่งเร้าพบว่า ให้ข้อมูลมากกว่าระยะเวลาระหว่างศักยะงานเอง แต่เวลาระหว่างศักยะงานก็ยังสามารถใช้เข้ารหัสข้อมูลอื่น ๆ และสำคัญเป็นพิเศษเมื่ออัตราการส่งสัญญาณถึงจุดยอด เช่นเมื่อสิ่งที่เห็นมีความเปรียบต่างสูง ด้วยเหตุนี้ รหัสโดยเวลาอาจมีบทบาทในการเข้ารหัสส่วนขอบของสิ่งที่เห็น (ที่มีความเปรียบต่างสูง) และไม่มีเมื่อสิ่งเร้าเปลี่ยนอย่างอย่างช้า ๆ หรือน้อย

ระบบรู้รสของสัตว์เลี้ยงลูกด้วยนมช่วยในการศึกษารหัสโดยเวลา เพราะสิ่งเร้าค่อนข้างต่าง ๆ กัน และสัตว์ก็ตอบสนองต่าง ๆ กันพอสังเกตได้ ข้อมูลที่เข้ารหัสโดยเวลาอาจช่วยสิ่งมีชีวิตให้จำแนกรสชาติต่าง ๆ ที่อยู่ในหมวดเดียวกัน (เช่น หวาน ขม เปรี้ยว เค็ม อุมะมิ) แม้อัตราศักยะงานจะเหมือนกัน ข้อมูลทางเวลาของรูปแบบการตอบสนองต่อรสชาติแต่ละอย่าง อาจใช้ระบุว่ามันคืออะไร (เช่น ความแตกต่างระหว่างรสขมสองอย่าง เช่นยาควินินและ Denatonium ที่ขมมาก) ดังนั้น ทั้งการเข้ารหัสโดยอัตราและโดยเวลาอาจจะใช้ในระบบรู้รส คือโดยอัตราสำหรับหมวดหมู่พื้นฐานของรสชาติ และโดยเวลาสำหรับรายละเอียดโดยเฉพาะอื่น ๆ

งานวิจัยในระบบรู้รสของสัตว์เลี้ยงลูกด้วยนมได้แสดงว่า มีข้อมูลจำนวนมากในรูปแบบตามกาลเวลาที่ใช้ในกลุ่มเซลล์ประสาทต่าง ๆ และเป็นข้อมูลที่ต่างจากที่เข้ารหัสโดยอัตรา กลุ่มเซลล์ประสาทอาจประสานส่งกระแสประสาทพร้อม ๆ กันเมื่อตอบสนองต่อสิ่งเร้าหนึ่ง ๆ

ในการศึกษาสมองกลีบหน้าของไพรเมต รูปแบบทางเวลาที่ละเอียดแม่นยำเป็นระยะเวลาสั้น ๆ เพียงไม่กี่มิลลิวินาทีจะพบทั่วกลุ่มเซลล์ประสาท ซึ่งมีสหสัมพันธ์กับพฤติกรรมเกี่ยวกับการแปลข้อมูลบางอย่าง แม้นักวิทยาศาสตร์ยังกำหนดรายละเอียดไม่ค่อยได้ แต่ก็อาจอธิบายได้ว่า เป็นผลพลอยได้ในระบบต่าง ๆ ของเปลือกสมองที่ใช้ข้อมูลขาเข้าร่วมกัน หรืออาจเพื่อเพิ่มความเร็วในการแปลผลของเปลือกสมองโดยไม่ได้ข้อมูลอะไรเพิ่ม

เหมือนกับระบบการเห็น ใน mitral cell ของป่องรับกลิ่นในหนูหริ่ง ระยะเวลาของศักยะงานแรกจากการดมกลิ่น (คือระยะแฝง) ดูเหมือนจะเข้ารหัสข้อมูลจำนวนมากเกี่ยวกับกลิ่น กลยุทธ์การใช้ระยะแฝงทำให้สามารถระบุกลิ่นและมีพฤติกรรมตอบสนองต่อกลิ่นนั้นได้เร็ว นอกจากนั้น mitral cell ยังมีรูปแบบการส่งสัญญาณโดยเฉพาะ ๆ ต่อกลิ่นต่าง ๆ ข้อมูลเช่นนี้อาจช่วยระบุกลิ่นบางชนิด แต่อาจไม่จำเป็นต้องมี เพราะอัตราของศักยะงานในช่วงที่สัตว์ดมกลิ่นก็สามารถทำให้ระบุกลิ่นได้แล้ว

ในแนวเดียวกัน งานทดลองในระบบรู้กลิ่นของกระต่ายแสดงการส่งสัญญาณในรูปแบบต่าง ๆ ที่มีสหสัมพันธ์กับกลิ่นต่าง ๆ และก็พบผลเช่นเดียวกันในงานทดลองกับตั๊กแตน

การประยุกต์ใช้

ความจำเพาะเจาะจงของรหัสโดยเวลา ทำให้ต้องใช้เทคโนโลยีที่ละเอียดมากในการวัดหาข้อมูลทางการทดลองที่ทั้งให้ความรู้และเชื่อถือได้ ความก้าวหน้าทางเทคนิค optogenetics ช่วยให้นักประสาทวิทยาศาสตร์สามารถควบคุมศักยะงานภายในนิวรอนหนึ่ง ๆ ได้โดยเฉพาะ ทำให้ควบคุมรูปแบบไฟฟ้าของศักยะงานและระยะเวลาระหว่างศักยะงานในระดับเซลล์เดี่ยว ๆ ได้ ยกตัวอย่างเช่น แสงสีน้ำเงินจะทำให้ช่องไอออนเปิดปิดด้วยแสง คือ channelrhodopsin เปิด ทำให้เซลล์ลดขั้วแล้วสร้างศักยะงาน เมื่อเซลล์ตรวจไม่พบแสงสีน้ำเงินอีก ช่องก็จะปิด แล้วเซลล์ก็จะหยุดส่งศักยะงาน รูปแบบของศักยะงานจะจับคู่กับรูปแบบของสิ่งเร้าคือแสงสีน้ำเงิน การใส่ลำดับยีนของ channelrhodopsin เข้าในดีเอ็นเอของหนูหริ่ง จึงทำให้นักวิจัยสามารถควบคุมศักยะงานและควบคุมพฤติกรรมบางอย่างของหนู (เช่น ทำให้หนูหันไปทางซ้าย) ได้ ผ่านเทคนิค optogenetics นักวิจัยจึงมีอุปกรณ์ที่สร้างผลต่อการเข้ารหัสโดยเวลาต่าง ๆ ในนิวรอน ในขณะที่ยังดำรงอัตราเฉลี่ยการยิงสัญญาณเท่า ๆ กัน และดังนั้น จึงสามารถทดสอบได้ว่า มีวงจรประสาทหนึ่ง ๆ ที่เข้ารหัสโดยเวลาหรือไม่

เทคโนโลยี Optogenetic มีโอกาสช่วยแก้ปัญหาการส่งศักยะงานที่เป็นมูลฐานของโรคทางประสาทและจิตหลายอย่าง ถ้าจริง ๆ นิวรอนเข้ารหัสข้อมูลในรูปแบบตามเวลาของศักยะงาน ข้อมูลสำคัญอาจจะมองข้ามไปเมื่อพยายามถอดรหัสจากแค่อัตราการยิงสัญญาณ การเข้าใจรหัสประสาทในรูปแบบตามเวลาและการทำซ้ำรูปแบบเหล่านี้ได้ในนิวรอน อาจจะทำให้ควบคุมและรักษาโรคในระบบประสาท เช่น โรคซึมเศร้า โรคจิตเภท และโรคพาร์คินสัน ได้ดีขึ้น เพราะการควบคุมระยะการส่งศักยะงานในเซลล์เดี่ยว ๆ จะทำให้ควบคุมการทำงานของสมองได้แม่นยำยิ่งกว่าการใช้ยา

การเข้ารหัสโดยเฟสที่ยิงสัญญาณ (Phase-of-firing code)

รหัสโดยเฟสที่ยิงสัญญาณ (Phase-of-firing code) เป็นรหัสทางประสาทที่รวมการเข้ารหัสโดยอัตรา กับจุดอ้างอิงทางเวลาซึ่งอาศัยการแกว่งกวัดของคลื่นสมอง (Neural oscillation) รหัสประเภทนี้มีป้าย/ข้อมูลเวลาสำหรับแต่ละศักยะงานโดยอ้างอิงเวลาตามเฟสการแกว่งกวัดของคลื่นประสาทเฉพาะที่ ๆ ไม่ว่าจะแบบความถี่ต่ำ หรือความถี่สูง ลักษณะอย่างหนึ่งของการเข้ารหัสนี้ก็คือ นิวรอนจะมีลำดับการยิงสัญญาณโดยเฉพาะ ๆ

มีงานศึกษาที่แสดงว่า นิวรอนในเปลือกสมองรับความรู้สึกบางส่วน เข้ารหัสสิ่งเร้าที่ซับซ้อนตามธรรมชาติโดยเวลาของศักยะงานที่เป็นไปตามเฟสของคลื่นสมองในพื้นที่ ไม่ใช่เป็นไปตามจำนวนศักยะงานเท่านั้น โดยคลื่นสมองจะสะท้อนศักย์สนามไฟฟ้าเฉพาะที่ (local field potential) นี่บ่อยครั้งจัดเป็นรหัสโดยเวลาแม้ป้ายเวลาที่ใช้กับศักยะงานจะค่อนข้างหยาบ

นั่นก็คือ ค่าวิยุต 4 ค่าสำหรับเฟสต่าง ๆ ก็พอใช้เป็นตัวแทนข้อมูลที่อยู่ในรหัสเช่นนี้ โดยหมายเอาเฟสของการกวัดแกว่งที่ความถี่ต่ำ รหัสโดยเฟสที่ยิงสัญญาณได้ไอเดียคร่าว ๆ จากปรากฏการณ์ Phase precession ใน place cell (เซลล์สถานที่) ที่ฮิปโปแคมปัส ซึ่งเป็นเซลล์ที่ทำงานเมื่อสัตว์ไปถึงสถานที่โดยเฉพาะ ๆ ภายในสิ่งแวดล้อม

การเข้ารหัสตามเฟสยังพบในเปลือกสมองส่วนการเห็นที่มีการกวัดแกว่งความถี่สูงด้วย ภายในรอบของการกวัดแกว่งพิสัยแกมมา (30-70&npbs;เฮิรตซ์) เซลล์ประสาทแต่ละตัวจะมีช่วงที่มักจะยิงสัญญาณ เพราะเหตุนี้ กลุ่มนิวรอนทั้งหมดจึงสร้างขบวนศักยะงานที่มีระยะยาวถึงประมาณ 15 มิลลิวินาที

การเข้ารหัสโดยกลุ่ม (Population coding)

การเข้ารหัสโดยกลุ่ม (Population coding) เป็นวิธีเข้ารหัสสิ่งเร้าโดยการทำงานร่วมกันของนิวรอนจำนวณหนึ่ง ในวิธีนี้ นิวรอนแต่ละเซลล์จะตอบสนองต่อสิ่งเร้าบางเซตแบบกระจายตัว และการตอบสนองของนิวรอนจำนวนหนึ่งรวมกันก็จะสามารถกำหนดค่าบางอย่างเกี่ยวกับสิ่งเร้า

จากมุมมองทางทฤษฎี การเข้ารหัสโดยกลุ่มเป็นเรื่องที่เข้าสูตรทางคณิตได้ค่อนข้างดีในบรรดาปัญหาทางประสาทวิทยาศาสตร์ทั้งหลาย มันรวมส่วนสำคัญต่าง ๆ ของการเข้ารหัสทางประสาท แต่ก็ยังวิเคราะห์ทางทฤษฎีได้ง่ายพอ งานศึกษาแบบทดลองได้แสดงว่า การเข้ารหัสแบบนี้ใช้อย่างกว้างขวางภายในเขตสมองส่วนรับความรู้สึก (sensory) และส่วนสั่งการ (motor)

ยกตัวอย่างเช่น ในเขตการเห็นของสมองกลีบขมับส่วนใน (Medial temporal lobe, MT) นิวรอนจะประมวลผลกำหนดโดยทิศทางที่สิ่งเร้าเคลื่อนที่โดยเฉพาะ ๆ. ในการตอบสนองต่อวัตถุที่กำลังเคลื่อนที่ไปยังทิศทางหนึ่งโดยเฉพาะ ๆ นิวรอนจำนวนมากใน MT จะยิงสัญญาณแบบมีเสียงรบกวน โดยมีรูปแบบเป็นระฆังคว่ำตลอดทั้งกลุ่ม แต่ทิศทางของวัตถุก็ยังสามารถกำหนดได้จากการทำงานของนิวรอนทั้งกลุ่ม ซึ่งทนต่อความผันผวนของสัญญาณจากนิวรอนเดี่ยว ๆ

ในตัวอย่างคลาสสิกตัวอย่างหนึ่งใน primary motor cortex นักวิจัยได้ฝึกลิงให้ขยับก้านควบคุมไปยังเป้าหมาย แล้วพบว่า นิวรอนหนึ่ง ๆ จะยิงสัญญาณตอบสนองต่อทิศทางการเคลื่อนที่ของเป้าหมายหลายทิศทาง แต่มันจะยิงสัญญาณที่อัตราสูงสุดในทิศทางเดียว และที่อัตราลดลงขึ้นอยู่กับว่า ทิศทางของเป้าหมายนั้นใกล้กับทิศทางซึ่งมันถนัดที่สุดมากเท่าไร

นักวิชาการคนหนึ่ง (Kenneth Johnson) ได้สรุปว่า ถ้านิวรอนแต่ละตัวเป็นตัวแทนการเคลื่อนไหวของสิ่งเร้าในทิศทางที่ตนถนัด การคำนวณรวมเวกเตอร์ของนิวรอนทั้งหมด โดยนิวรอนแต่ละตัวมีอัตราการยิงสัญญาณและทิศทางที่ตนถนัดโดยเฉพาะ ๆ ก็จะแสดงทิศทางการเคลื่อนที่ของสิ่งเร้า ดังนั้น การทำงานของกลุ่มนิวรอนจึงเข้ารหัสทิศทางการเคลื่อนที่ของสิ่งเร้า การเข้ารหัสเช่นนี้มีชื่อเฉพาะว่า population vector coding

นักวิชาการอีกลุ่มหนึ่งได้พัฒนารหัสโดยกลุ่มตามสถานที่-เวลา ซึ่งเรียกว่า Averaged-Localized-Synchronized-Response (ALSR) code โดยเป็นการเข้ารหัสสิ่งเร้าทางหูคือเสียง และใช้ข้อมูลเกี่ยวกับนิวรอนที่ตอบสนองต่อจุดที่เป็นแหล่งเสียงโดยเฉพาะ ๆ ในโสตประสาท (auditory nerve) กับการยิงสัญญาณจับคู่กับเฟสภายในโสตประสาท การเข้ารหัสดั้งเดิมใช้ได้กับเสียงสระแบบไม่เปลี่ยนเสียง ต่อมาจึงใช้ได้กับพยางค์ที่ประกอบด้วยพยัญชนะ-สระ โดยรวมความสูงต่ำของเสียง (pitch) และความถี่สั่นพ้อง (formant) ที่ซับซ้อนและอาจเปลี่ยนเสียงในระหว่าง (non steady state)

การเข้ารหัสโดยกลุ่มยังมีข้อดีอื่น ๆ อีกด้วย รวมทั้งการลดความไม่แน่นอนเนื่องจากความผันแปรได้ทางสถิติ และสมรรถภาพในการเป็นตัวแทนลักษณะสิ่งเร้าต่าง ๆ พร้อม ๆ กัน วิธีนี้ยังเร็วกว่าการเข้ารหัสโดยอัตรา และสามารถสะท้อนความเปลี่ยนแปลงของสิ่งเร้าได้แทบทันที นิวรอนแต่ละตัวในกลุ่มมักจะตอบสนองสิ่งเร้าที่ต่าง ๆ แต่คาบเกี่ยวกัน ดังนั้น นิวรอนจำนวนหนึ่งแต่ไม่ทั้งหมดก็จะตอบสิ่งเร้าหนึ่ง ๆ

โดยปกติแล้ว ฟังก์ชันการเข้ารหัสจะมีค่าสูงสุด เมื่อการทำงานของนิวรอนนั้น ๆ อยู่ในระดับสูงสุด และก็จะลดลงตามลำดับค่าที่ไม่ใช่เป็นจุดยอด ดังนั้น ระดับการรับรู้สิ่งเร้าจึงสามารถคำนวณได้จากรูปแบบการทำงานทั่วไปของกลุ่มนิวรอน

population vector coding ที่กล่าวถึงมาก่อนเป็นตัวอย่างของการหาค่าเฉลี่ยธรรมดา ๆ เทคนิคทางคณิตศาสตร์ที่ซับซ้อนกว่ารวมวิธีค่าควรจะเป็นสูงสุด (maximum likelihood) อาศัยการแจกแจงหลายตัวแปร (multivariate distribution) ของการตอบสนองของนิวรอน แบบจำลองเหล่านี้อาจสมมุติความเป็นอิสระ หรือสหสัมพันธ์แบบทุติยภูมิ หรือแม้แต่ภาวะพึ่งพิงที่ซับซ้อนอย่างเช่น higher order maximum entropy probability distribution หรือ Copula

การเข้ารหัสโดยสหสัมพันธ์ (Correlation coding)

แบบจำลองการเข้ารหัสโดยสหสัมพันธ์เสนอว่า มีสหสัมพันธ์ระหว่างศักยะงานภายในขบวน ซึ่งอาจเป็นข้อมูลนอกเหนือไปจากระยะเวลาธรรมดาระหว่างศักยะงานต่าง ๆ งานวิจัยปี 2523 แสดงว่า สหสัมพันธ์ระหว่างขบวนศักยะงานจะสามารถลด แต่ไม่สามารถเพิ่มข้อมูลที่พึ่งพาอาศัยกัน (mutual information) ที่มีในขบวนศักยะงาน 2 ขบวน โดยเกี่ยวกับลักษณะหนึ่งของสิ่งเร้า แต่งานปี 2542 แสดงว่าไอเดียนี้ไม่ถูกต้อง โครงสร้างโดยสหสัมพันธ์จะสามารถเพิ่มข้อมูลที่มี ถ้าค่าสหสัมพันธ์ของเสียงรบกวนและของสัญญาณ/ข้อมูลมีเครื่องหมายตรงกันข้ามกัน

ค่าสหสัมพันธ์สามารถให้ข้อมูลที่ไม่ได้อยู่ในอัตราการยิงสัญญาณโดยเฉลี่ยของนิวรอนสองคู่ ตัวอย่างหนึ่งก็คือ เปลือกสมองส่วนการได้ยินของมาโมเสทที่ได้ยาชาแล้ว ซึ่งเสียงโทนเดียวจะทำให้เกิดศักยะงานที่มีสหสัมพันธ์กันจำนวนมากขึ้น แต่ก็ไม่ได้เพิ่มอัตราการยิงสัญญาณโดยเฉลี่ยระหว่างนิวรอนเป็นคู่ ๆ

การเข้ารหัสโดยศักยะงานอิสระ (Independent-spike coding)

แบบจำลองการเข้ารหัสโดยศักยะงานอิสระเสนอว่า ศักยะงานแต่ละพัลส์เป็นอิสระจากกันและกันภายในขบวนศักยะงาน

การเข้ารหัสโดยตำแหน่ง (Position coding)

กราฟของการเข้ารหัสโดยตำแหน่งทั่ว ๆ ไป

การตอบสนองในระบบประสาทมีเสียงรบกวนมากและเชื่อถือไม่ค่อยได้

การเข้ารหัสโดยกลุ่มปกติจะเกี่ยวกับกลุ่มเซลล์ประสาทที่ตอบสนองโดยมี tuning curve เป็นฟังก์ชัน Gaussian ที่มีค่าคาดหมายหรือค่าเฉลี่ยซึ่งแปรผันแบบเชิงเส้นตามระดับสิ่งเร้า ซึ่งหมายความว่า เซลล์จะตอบสนองด้วยศักยะงานในอัตราสูงสุดต่อสิ่งเร้าที่มีระดับใกล้กับค่าคาดหมาย ดังนั้น ระดับของสิ่งเร้าจึงสามารถหาได้จากค่าคาดหมายของเซลล์ประสาทที่ตอบสนองในระดับสูงสุด แต่เพราะเสียงรบกวนที่มีโดยธรรมชาติในการตอบสนอง การประมาณค่าควรจะเป็นสูงสุด (maximum likelihood estimation) จะเป็นวิธีที่แม่นยำกว่า

การเข้ารหัสเช่นนี้จะใช้สำหรับตัวแปรแบบต่อเนื่องเช่น ตำแหน่งข้อต่อ ตำแหน่งตา สี หรือความถี่เสียง แม้นิวรอนเดี่ยว ๆ จะสร้างเสียงรบกวนมากเกินกว่าจะสามารถเข้ารหัสตัวแปรโดยอัตรา แต่กลุ่มนิวรอนรวมกันก็สามารถให้ข้อมูลที่เชื่อถือได้และแม่นยำกว่า สำหรับกลุ่มนิวรอนที่มี tuning curve แบบมียอดเดียว ความแม่นยำปกติจะดีขึ้นในเชิงเส้นตามจำนวนของเซลล์ประสาท ดังนั้น สำหรับความแม่นยำครึ่งหนึ่ง ก็จะใช้นิวรอนจำนวนครึ่งเดียว เทียบกับ tuning curve แบบมีหลายยอด ดังที่พบใน grid cell ในสมองของสัตว์หลายสปีชีส์ เป็นเซลล์ซึ่งเข้ารหัสข้อมูลเกี่ยวกับปริภูมิรอบ ๆ ตัวสัตว์ ความแม่นยำที่ได้จากกลุ่มนิวรอนเช่นนี้ จะเพิ่มขึ้นแบบยกกำลังตามจำนวนเซลล์ประสาท ซึ่งลดจำนวนนิวรอนได้อย่างมหาศาลเพื่อให้ได้ความแม่นยำเท่ากัน

การเข้ารหัสแบบน้อยเซลล์ (Sparse coding)

การเข้ารหัสแบบน้อยเซลล์ก็คือลักษณะสิ่งเร้าแต่ละอย่างจะเข้ารหัสโดยการทำงานอย่างเต็มที่ของนิวรอนเป็นจำนวนน้อย คือ จะมีกลุ่มนิวรอนย่อย ๆ ที่ทำงานตอบสนองต่อลักษณะสิ่งเร้าที่ต่างกัน

ถึงกระนั้น "ความน้อย" ก็อาจจะเป็นทางเวลา คือ "จะทำงานเป็นช่วงเวลาค่อนข้างน้อย" หรืออาจจะหมายถึงจำนวนนิวรอนที่ทำงานตอบสนองภายในกลุ่ม ในกรณีหลัง จึงอาจนิยามได้ว่าเป็นจำนวนนิวรอนที่ทำงานเปรียบเทียบกับจำนวนนิวรอนทั้งหมดภายในกลุ่มในช่วงระยะเวลาหนึ่ง นี่ดูเหมือนจะเป็นเอกลักษณ์ของการแปลผลทางประสาทเมื่อเปรียบเทียบกับคอมพิวเตอร์ดั้งเดิม เพราะข้อมูลจะกระจายตัวไปอย่างกว้างขวางไปทั่วกลุ่มนิวรอน งานวิจัยปี 2539 แสดงว่า การเข้ารหัสแบบน้อยเซลล์ของรูปภาพต่าง ๆ ตามธรรมชาติ จะสร้างฟิลเตอร์คล้ายกับ wavelet ซึ่งก็คล้ายกับลานรับสัญญาณของเซลล์ธรรมดา ๆ ในเปลือกสมองส่วนการเห็น ความจุของการเข้ารหัสเช่นนี้อาจเพิ่มโดยใช้การเข้ารหัสโดยเวลาพร้อม ๆ กัน ดังที่พบในระบบรู้กลิ่นของตั๊กแตน

เพราะสิ่งเร้ามีรูปแบบต่าง ๆ มากมาย ขั้นตอนวิธีการเข้ารหัสแบบน้อยเซลล์จะพยายามสืบหารูปแบบจำนวนน้อยที่เป็นตัวแทน (representative patterns) อย่างอัตโนมัติ ซึ่งเมื่อรวมรูปแบบในสัดส่วนที่ถูกต้อง ก็จะสามารถเป็นตัวแทนของสิ่งเร้าที่ปรากฏ ดังนั้น รหัสโดยน้อยเซลล์ของสิ่งเร้าก็คือรูปแบบที่เป็นตัวแทนเหล่านี้ ยกตัวอย่างเช่น ประโยคมากมายในภาษาไทยสามารถเข้ารหัสเป็นเครื่องหมายต่าง ๆ ซึ่งมีจำนวนน้อย (เช่น อักษร วรรณยุกต์ ตัวเลข และวรรค) โดยรวมกันเป็นลำดับอย่างเฉพาะเจาะจงเพื่อเป็นตัวแทนประโยคหนึ่ง ๆ ในนัยเดียวกัน การเข้ารหัสแบบน้อยเซลล์ก็จะเป็นเหมือนกับเครื่องหมายเหล่านี้

Linear generative model

แบบจำลองของการเข้ารหัสแบบน้อยเซลล์มักจะเป็นแบบ linear generative model (แบบจำลองเพิ่มพูนเชิงเส้น) ในแบบจำลองนี้ เครื่องหมายจะรวมกันแบบผลรวมเชิงเส้นเพื่อประมาณข้อมูลขาเข้า

โดยรูปนัยก็คือ สำหรับเซตเวกเตอร์จำนวนจริงที่เป็นข้อมูลเข้าและมีมิติ k (k-dimensional set of real-numbered input vectors) คือ ${\displaystyle {\vec {\xi }}\in \mathbb {R} ^{k}}$

เป้าหมายของการเข้ารหัสโดยน้อยเซลล์ก็คือเพื่อกำหนดเวกเตอร์ฐานหลักที่มีมิติ k และมีจำนวน n (n k-dimensional basis vectors) คือ ${\displaystyle {\vec {b_{1}}},\ldots ,{\vec {b_{n}}}\in \mathbb {R} ^{k}}$ พร้อมกับเวก์เตอร์มากเลขศูนย์ที่มีมิติ n (sparse n-dimensional vector) เวกเตอร์หนึ่ง ${\displaystyle {\vec {s}}\in \mathbb {R} ^{n}}$ ที่เป็นน้ำหนักหรือสัมประสิทธิ์สำหรับแต่ละเวกเตอร์ขาเข้า เพื่อให้ผลรวมเชิงเส้นของเวกเตอร์ฐานหลักในสัดส่วนที่กำหนดโดยสัมประสิทธิ์ มีผลเป็นค่าใกล้ ๆ กับเวกเตอร์ขาเข้า คือ ${\displaystyle {\vec {\xi }}\approx \sum _{j=1}^{n}s_{j}{\vec {b}}_{j}}$

รหัสที่สร้างโดยขั้นตอนวิธีที่ดำเนินการด้วย linear generative model อาจจัดเป็นสองอย่างคือแบบ soft sparseness (น้อยผ่อน ๆ) และ hard sparseness (น้อยจริง ๆ) โดยแบบ 2 อย่างจะมุ่งหมายการกระจายตัวของสัมประสิทธิ์ของเวกเตอร์ฐานหลักสำหรับข้อมูลเข้าทั่วไป

• รหัสแบบน้อยผ่อน ๆ จะมีการกระจายตัวคล้าย Gaussian เรียบ ๆ แม้จะแหลมกว่าเส้นโค้ง Gaussian โดยมีค่า 0 มาก, มีค่าสัมบูรณ์ต่ำ ๆ บ้าง, มีค่าสัมบูรณ์สูง ๆ น้อยกว่า, และมีความสัมบูรณ์สูงมากน้อยมาก ดังนั้น เวกเตอร์ฐานหลักจำนวนมากจึงไม่ใช่ศูนย์คือยังให้ผลอยู่
• เทียบกับรหัสแบบน้อยจริง ๆ ซึ่งมีค่า 0 มาก, ไม่มีหรือเกือบไม่มีค่าสมบูรณ์ต่ำ, มีค่าสัมบูรณ์ที่มากขึ้นน้อยกว่า, และมีค่าสัมบูรณ์สูงมากน้อยมาก ดังนั้น เวกเตอร์ฐานหลักจำนวนน้อยมากก็จะมีค่ามากกว่า 0 ซึ่งได้เปรียบจากมุมมองของเมแทบอลิซึม เพราะการทำงานของนิวรอนที่มีจำนวนน้อยกว่าก็จะใช้พลังงานน้อยกว่า

รหัสนี้อาจแบ่งได้โดยอีกวิธีหนึ่งเป็น 2 แบบ ก็คือแบบ critically complete (สมบูรณ์อย่างวิกฤติ) หรือ overcomplete (สมบูรณ์เกิน)

• ถ้าจำนวนเวกเตอร์ฐานหลักคือ n เท่ากับ k ซึ่งเป็นมิติของเซตข้อมูลเข้า การเข้ารหัสนี้เรียกว่า สมบูรณ์อย่างวิกฤติ ในกรณีนี้ การเปลี่ยนแปลงเล็ก ๆ น้อย ๆ ของเวกเตอร์ข้อมูลเข้า จะทำให้สัมประสิทธิ์เปลี่ยนโดยฉับพลัน ดังนั้น รหัสจึงไม่สามารถรองรับการการเปลี่ยนสเกล การเลื่อนที่ หรือเสียงรบกวนเล็ก ๆ น้อย ๆ ในข้อมูลขาเข้า
• แต่ถ้าเวกเตอร์ฐานหลักมีจำนวนมากกว่ามิติของเซตข้อมูลเข้า รหัสก็จะจัดว่า สมบูรณ์เกิน และรหัสที่สมบูรณ์เกินจะเปลี่ยนค่าได้อย่างเรียบ ๆ สำหรับเวกเตอร์ข้อมูลเข้าที่มีค่าในระหว่าง ๆ และทนทานต่อเสียงรบกวนได้ดี

เปลือกสมองส่วนการเห็นปฐมภูมิของมนุษย์ประเมินว่า สมบูรณ์เกินโดยแฟกเตอร์ 500 ดังนั้น ข้อมูลขาเข้าที่ 14x14 (196-dimensional space) จะเข้ารหัสโดยนิวรอนประมาณ 100,000 ตัว

หลักฐานทางชีววิทยา

การเข้ารหัสโดยน้อยเซลล์ อาจเป็นกลยุทธ์ทั่วไปของระบบประสาทเพื่อเพิ่มความจุของความจำ คือ เพื่อปรับตัวให้เข้ากับสิ่งแวดล้อม สัตว์จะต้องเรียนรู้ว่า สิ่งเร้าเช่นไรสัมพันธ์กับรางวัลหรือการลงโทษ แล้วจำแนกสิ่งเร้าที่เสริมแรงเช่นนี้จากสิ่งเร้าที่คล้ายกันแต่ไม่เกี่ยวกัน ปฏิบัติการเช่นนี้จะต้องมีหน่วยความจำสาระ (associative memory) ที่เฉพาะเจาะจงต่อสิ่งเร้า ที่นิวรอนไม่กี่ตัวจากทั้งกลุ่มจะตอบสนองต่อสิ่งเร้าหนึ่ง ๆ และนิวรอนแต่ละตัว ๆ จะตอบสนองต่อสิ่งเร้าไม่กี่อย่างจากสิ่งเร้าที่เป็นไปได้ทั้งหมด

งานทฤษฎีเรื่อง Sparse distributed memory (ความจำแบบกระจายและมากไปด้วยศูนย์) ได้เสนอว่า การเข้ารหัสโดยน้อยเซลล์จะเพิ่มความจุของความจำสาระ โดยลดความคาบเกี่ยวกันระหว่างการทำงานของนิวรอนที่เป็นตัวแทนลักษณะสิ่งเร้า ส่วนในงานทดลอง การเข้ารหัสโดยน้อยเซลล์ของข้อมูลความรู้สึก ได้พบในระบบรับความรู้สึกหลายอย่างรวมทั้งระบบการเห็นระบบการได้ยิน ระบบรู้สัมผัส และระบบรู้กลิ่น

อย่างไรก็ดี แม้จะมีหลักฐานเพิ่มขึ้นเรื่อย ๆ เกี่ยวกับการใช้รหัสเช่นนี้อย่างกว้างขวางในระบบประสาท รวมทั้งข้อสนับสนุนทางทฤษฎีเกี่ยวกับความสำคัญของมัน งานที่แสดงว่า รหัสโดยน้อยเซลล์จะเพิ่มความเฉพาะเจาะจงต่อสิ่งเร้าของระบบความจำสาระก็ไม่ค่อยมีจนกระทั่งเร็ว ๆ นี้

ในปี 2557 นักกายวิภาคชาวสวีเดน-อังกฤษ (Gero Miesenböck) ที่มหาวิทยาลัยออกซฟอร์ดได้ทำงานวิเคราะห์กับระบบรู้กลิ่นของแมลงวันทอง ในแมลงวันทอง การเข้ารหัสกลิ่นโดยน้อยเซลล์ของ Kenyon cell ใน Mushroom bodies เชื่อว่า จะเป็นตัวกำหนดตำแหน่งแบบเข้าเลขอย่างแม่นยำจำนวนมากเพื่อบรรจุความจำเกี่ยวกับกลิ่นโดยเฉพาะ ๆ

งานวิจัยอีกงานปี 2557 แสดงว่า ความมากน้อยของนิวรอนที่ทำงาน (sparseness) จะควบคุมโดยวงจรป้อนกลับเชิงผกผันระหว่าง Kenyon cells และ GABAergic anterior paired lateral (APL) neuron การจงใจกระตุ้นและหยุดการทำงานอย่างเป็นระบบของส่วนแต่ละส่วนในวงจรนี้แสดงว่า Kenyon cells จะกระตุ้นให้ APL ทำงาน และในทางกลับกัน APL ก็จะยับยั้ง Kenyon cells ไม่ให้ทำงาน การระงับวงจรป้อนกลับ Kenyon cell-APL จะกวนการเข้ารหัสแบบน้อยเซลล์ที่ตอบสนองต่อกลิ่นของ Kenyon cell, เพิ่มสหสัมพันธ์ในระหว่างกลิ่นต่าง ๆ, และกันแมลงวันไม่ให้เรียนรู้แยกแยะกลิ่นที่คล้ายกัน แต่ไม่กันสำหรับกลิ่นที่ต่างกัน ผลเช่นนี้แสดงว่า การยับยั้งแบบป้อนกลับที่ระงับการทำงานของ Kenyon cell ทำให้สามารถดำรงการเข้ารหัสกลิ่นอย่างน้อยเซลล์ แยกแยะไม่ให้ปนกลิ่น และดังนั้น ดำรงความเฉพาะเจาะจงต่อกลิ่นในระบบความจำ

ดูเพิ่ม

• โครงข่ายประสาทเทียม
• การเรียนรู้เชิงลึก

เชิงอรรถ

แหล่งข้อมูลอื่น

• Foldiak P, Endres D, Sparse coding, Scholarpedia, 3 (1) :2984, 2008.
• Dayan P & Abbott LF. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Cambridge, Massachusetts: The MIT Press; 2001. ISBN 0-262-04199-5
• Rieke F, Warland D, de Ruyter van Steveninck R, Bialek W. Spikes: Exploring the Neural Code. Cambridge, Massachusetts: The MIT Press; 1999. ISBN 0-262-68108-0
• Tsien, JZ.; และคณะ (2014). "On initial Brain Activity Mapping of episodic and semantic memory code in the hippocampus". Neurobiology of Learning and Memory. 105: 200–210. doi:10.1016/j.nlm.2013.06.019.